一、“树”是一种重要的数据结构,本文浅谈二叉树的遍历问题,采用C语言描述。 1)定义:有且仅有一个根结点,除根节点外,每个结点只有一个父结点,最多含有两个子节点,子节点有左右之分。 2)存储结构 二叉树的存储结构可以采用顺序存储,也可以采用链式存储,其中链式存储更加灵活。 在链式存储结构中,与线性链表类似,二叉树的每个结点采用结构体表示,结构体包含三个域:数据域、左指针、右指针。
struct BiTreeNode{
int c;
struct BiTreeNode *left;
struct BiTreeNode *right;
};
二、二叉树的遍历 “遍历”是二叉树各种操作的基础。二叉树是一种非线性结构,其遍历不像线性链表那样容易,无法通过简单的循环实现。 二叉树是一种树形结构,遍历就是要让树中的所有节点被且仅被访问一次,即按一定规律排列成一个线性队列。二叉(子)树是一种递归定义的结构,包含三个部分:根结点(N)、左子树(L)、右子树(R)。根据这三个部分的访问次序对二叉树的遍历进行分类,总共有6种遍历方案:NLR、LNR、LRN、NRL、RNL和LNR。研究二叉树的遍历就是研究这6种具体的遍历方案,显然根据简单的对称性,左子树和右子树的遍历可互换,即NLR与NRL、LNR与RNL、LRN与RLN,分别相类似,因而只需研究NLR、LNR和LRN三种即可,分别称为“先序遍历”、“中序遍历”和“后序遍历”。 二叉树遍历通常借用“栈”这种数据结构实现,有两种方式:递归方式及非递归方式。 在递归方式中,栈是由操作系统维护的,用户不必关心栈的细节操作,用户只需关心“访问顺序”即可。因而,采用递归方式实现二叉树的遍历比较容易理解,算法简单,容易实现。 递归方式实现二叉树遍历的C语言代码如下:
//先序遍历--递归
int traverseBiTreePreOrder(BiTreeNode \*ptree,int (\*visit)(int))
{
if(ptree)
{
if(visit(ptree->c))
if(traverseBiTreePreOrder(ptree->left,visit))
if(traverseBiTreePreOrder(ptree->right,visit))
return 1; //正常返回
return 0; //错误返回
}else return 1; //正常返回
}
//中序遍历--递归
int traverseBiTreeInOrder(BiTreeNode \*ptree,int (\*visit)(int))
{
if(ptree)
{
if(traverseBiTreeInOrder(ptree->left,visit))
if(visit(ptree->c))
if(traverseBiTreeInOrder(ptree->right,visit))
return 1;
return 0;
}else return 1;
}
//后序遍历--递归
int traverseBiTreePostOrder(BiTreeNode \*ptree,int (\*visit)(int))
{
if(ptree)
{
if(traverseBiTreePostOrder(ptree->left,visit))
if(traverseBiTreePostOrder(ptree->right,visit))
if(visit(ptree->c))
return 1;
return 0;
}else return 1;
}二叉树的遍历有三种方式,如下: (1)前序遍历(DLR),首先访问根结点,然后遍历左子树,最后遍历右子树。简记根-左-右。 (2)中序遍历(LDR),首先遍历左子树,然后访问根结点,最后遍历右子树。简记左-根-右。 (3)后序遍历(LRD),首先遍历左子树,然后遍历右子树,最后访问根结点。简记左-右-根。 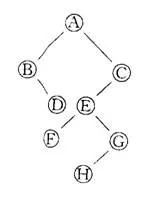 例1:如上图所示的二叉树,若按前序遍历,则其输出序列为 。若按中序遍历,则其输出序列为 。若按后序遍历,则其输出序列为 。 前序:根A,A的左子树B,B的左子树没有,看右子树,为D,所以A-B-D。再来看A的右子树,根C,左子树E,E的左子树F,E的右子树G,G的左子树为H,没有了结束。连起来为C-E-F-G-H,最后结果为ABDCEFGH 中序:先访问根的左子树,B没有左子树,其有右子树D,D无左子树,下面访问树的根A,连起来是BDA。 再访问根的右子树,C的左子树的左子树是F,F的根E,E的右子树有左子树是H,再从H出发找到G,到此C的左子树结束,找到根C,无右子树,结束。连起来是FEHGC, 中序结果连起来是BDAFEHGC 后序:B无左子树,有右子树D,再到根B。再看右子树,最下面的左子树是F,其根的右子树的左子树是H,再到H的根G,再到G的根E,E的根C无右子树了,直接到C,这时再和B找它们其有的根A,所以连起来是DBFHGECA
例1:如上图所示的二叉树,若按前序遍历,则其输出序列为 。若按中序遍历,则其输出序列为 。若按后序遍历,则其输出序列为 。 前序:根A,A的左子树B,B的左子树没有,看右子树,为D,所以A-B-D。再来看A的右子树,根C,左子树E,E的左子树F,E的右子树G,G的左子树为H,没有了结束。连起来为C-E-F-G-H,最后结果为ABDCEFGH 中序:先访问根的左子树,B没有左子树,其有右子树D,D无左子树,下面访问树的根A,连起来是BDA。 再访问根的右子树,C的左子树的左子树是F,F的根E,E的右子树有左子树是H,再从H出发找到G,到此C的左子树结束,找到根C,无右子树,结束。连起来是FEHGC, 中序结果连起来是BDAFEHGC 后序:B无左子树,有右子树D,再到根B。再看右子树,最下面的左子树是F,其根的右子树的左子树是H,再到H的根G,再到G的根E,E的根C无右子树了,直接到C,这时再和B找它们其有的根A,所以连起来是DBFHGECA